Implied Volatility In Options Trading: All You Need to Know

Implied volatility (IV) in the market refers to the forecasted magnitude, or one standard deviation (SD) range, of potential movement away from the underlying price in a year's time.

IV is not a guaranteed metric, but it’s helpful in traders understanding ranges from a statistical perspective to help with risk management, buying power etc

Low implied volatility environments tell us that the market isn’t expecting the stock price to move much from the current stock price over the course of a year. Whereas, a high implied volatility environment tells us that the market is expecting large movements from the current stock price over the course of the next twelve months.

Implied volatility is an annualized expected move in the underlying stocks price, adjusted for the expiration duration.

The tastytrade platform displays IV in several useful areas on its interface. One of them is to simply view volatility by expiration in the trade tab. The example below shows monthly expirations for SPY over the next 365 days. The +- number is the expected move of the underlying price given the current implied volatility percentage (IV%), adjusted for the expiration timeframe.

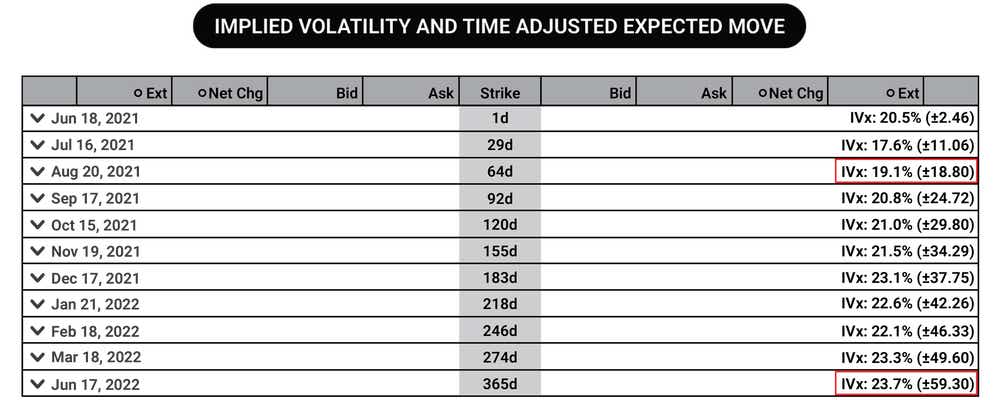
In the SPY example above, we see that over the next 64 days, the market is expecting a 19.1% implied volatility, which translates to an implied $18.80 range above or below the current stock price of $423.00. In other words, the current implied volatility and timeframe implies a $37.60 potential range from the current stock price, or between $404.20 and $441.80.

Over the course of 365 days, the implied volatility is 23.7%, which implies a move of ± $59.30 above or below the current stock price of $423.00, that’s a range of $118.60, or between $363.70 and $482.30.

Explore more IV examples

Implied volatility involves using a mathematical formula to forecast the likely movement of a stock. It’s important to note that implied volatility cannot predict the direction in which the price change will proceed – in other words, whether the price will go up, down or see-saw between the two variables or go beyond. It can only forecast the likely movement level in a security’s price.

Implied volatility can be used to determine a stock’s expected move over a given expiration cycle. You can find the implied volatility of a stock for different expirations using the Black-Scholes model. These implied ranges are based on annual expected moves by default.

At tastylive, we use the ‘expected move formula’, which allows us to calculate the one standard deviation range of a stock. This is based on the days to expiration (DTE) of our option contract, the stock price, and the stock's implied volatility.

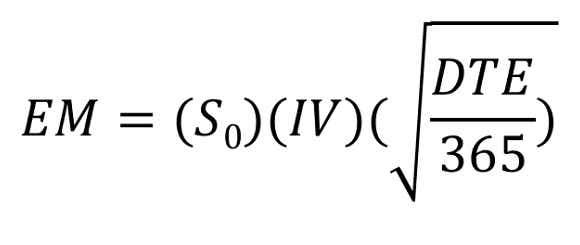EM = 1SD expected move S = stock price IV = implied volatility of your option’s expiration cycle DTE = days to expiration of your option contract

For example, the 1SD expected move of a $100 stock with an IV percentage of 20% is around $20 of the current stock price, or a range between $80 and $120.

Before diving into how this impacts options trading, it’s important to understand the probabilities associated with certain multiples of standard deviations:

1SD of a stock encompasses approximately 68.2% of outcomes in a distribution of occurrences based on current implied volatility 

2SD of a stock encompasses approximately 95.4% of outcomes in a distribution of occurrences based on current implied volatility

3SD of a stock encompasses approximately 99.7% of outcomes in a distribution of occurrences based on current implied volatility

Think of any stock (or underlying product) you like, and consider tracking how many times in a row it goes up in price, or down in price, for consecutive days. Over a large window of time, you’ll see that the vast majority of stock price movement would land in the 1SD range of outcomes, or 68.2% of the time. And 95.4% of the time with a 2SD range and 99.7% with a 3SD range.

This may be something like 1-3 days in a row moving in the same direction. Going out to 2SD would certainly have fewer occurrences and would track something like 4-7 days in a row moving in the same direction. 3SD would encompass the fewest occurrences of 7+ days in a row moving in the same direction.

The highest number of occurrences will generally encompass what we expect, and the lowest number of occurrences will encompass outlier events sometimes called a black swan.

• A low IV tells us that the market isn’t expecting the current stock price to move much over the course of a year or a given timeframe
• A high IV tells us that the market is expecting large movements from the current stock price over the next 12 months
• When equity prices decline over time, It’s called a bearish market, which is riskier for long-term bullish investors. In this type of market, implied volatility is likely to increase
• When prices rise over time, it’s referred to as a bullish market and IV is more likely to decrease

Implied volatility affects options by being one of the deciding factors in its pricing, as it estimates the future value of an option while considering its current value. Implied volatility is a measure of perceived volatility, so it’s important to keep an eye on it so that you know what kind of product you’re trading straight off the bat.

Implied volatility gives us context around option prices and what those prices predict in terms of potential stock price movements. This context is especially helpful for earnings trades, where you’re estimating the expected effect of the earnings announcement and strategizing around that.

Implied volatility can be used in several ways when trading options, including:

• Determining option prices
• Calculating the expected move of the underlying asset
• Measuring directional risk

High IV products tend to move around a lot, even if it isn’t in one direction, so it’s important to consider this when factoring in risk or determining an options strategy.

Conversely, high IV products offer higher extrinsic value premiums than low IV products, which is why short premium options traders tend to be drawn to it. Low IV environments equate to lower priced options due to a lack of extrinsic value; and high IV environments equate to higher priced options due to the abundance of extrinsic value.

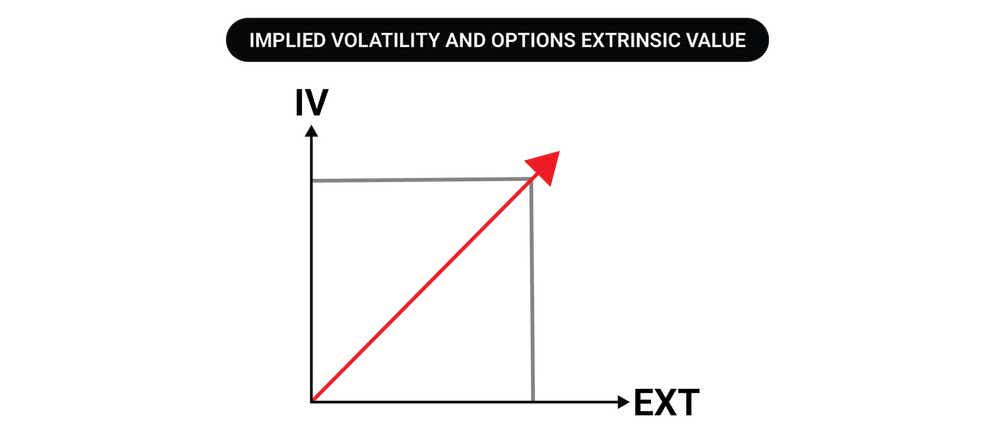
IV and extrinsic value in options prices always share a positive relationship.

• Higher extrinsic value in an options prices leads to higher implied volatility and lower option prices lead to lower implied volatility
• The buyer of a call and seller of a put could potentially make larger intrinsic value profits from higher IV if the stock moves up in a big way quickly
• The buyer of a put and seller of a call could potentially suffer larger losses from higher IV if the stock moves up in a big way quickly
• Time is working against a long option holder, which means each day the underlying doesn't get closer to their strike or past it, the long holder is relying on an extreme move to make up for lost time value
• If there’s a high demand for an option, the extrinsic value premium will rise, which drives implied volatility higher
  

Options pricing that you see, analyze and trade are controlled by sophisticated mathematical models. These models are not necessary to master as they’re built into the platforms you use for trading. In this section, we’re going to look at the Black-Scholes model, and the Binomial model.

To use implied volatility in options trading, follow these steps:

Determine whether implied volatility is high or low

Research why some options yield expensive premiums

Identify options with high IV that could be an options premium selling opportunity

Identify options with low IV that could be a premium buying opportunity

When you grasp how to use implied volatility, you’ll have a higher probability of success. After all, you want to minimize your risk and maximize your return as an investor. Understanding what implied volatility is telling you about a stock’s expected future movements is invaluable. It can greatly impact your strike choices, breakeven prices, max profit implications, and even your options trading strategy altogether, depending on how high or low IV is.

To understand how to use implied volatility, and then work out a strategy around it, you first need to grasp what IV levels can and cannot tell you.

 Determine Whether Implied Volatility Is High Or Low

Determine whether IV is high or low, rising or falling, by looking at a metrics that shows the IV rank.

Many option traders will look at high or low IV when they choose an investment opportunity. This information can then be used in several ways, including:

• Determine when the underlying options are relatively cheap or expensive
• Help you predefine your trading conditions and know when to enter or exit your position
• Decide when to invest in more stable products, for instance during periods of high volatility
• 
  Buy perceived undervalued options and sell perceived overvalued options
• Selling premium in high implied volatility environments to try to improve breakevens (compared to selling premium in low IV)

Implied volatility moves in cycles and traders need to monitor when IV reaches extreme highs or lows. In these instances, it’s expected to revert to its mean as it has shown mean reversion characteristics, historically speaking. This is just one aspect of options pricing though – a big directional move can offset this potential IV contraction.

 Research Why Some Options Yield Higher Premiums

There will always be a reason why some options yield higher premiums due to high implied volatility. It could be a product approval, or news about a merger or acquisition. Typically, just before earnings announcements, the IV will plateau; then, after the event, it’s most likely to drop and revert to its mean.

You’ll need to do some research by keeping an eye on any stock market announcements, or other major news events to determine why option prices are higher and why there’s suddenly such a high demand for it. This could help you in gauging when it’s a good time to buy or sell.


Finding a potentially advantageous opportunity can be a key part of enhancing your position’s probability of success. 

tastytrade empowers you to do this with tools such as:

• Our Follow Feed
• In-platform video feed
• Market watchlists

 Identifying Options With High Implied Volatility For Short Premium Strategies

After you’ve done your research, you could identify options with high implied volatility that you might consider selling. You can sell options and still be bullish or neutral. As we mentioned before, this can improve your breakeven (compared to selling premium in low implied volatility environments).

In high IV environments, you can consider options selling strategies such as:

• Credit spreads
• Naked puts
• Short straddles/strangles
• Covered calls

Let’s take a look at an example using high IV.

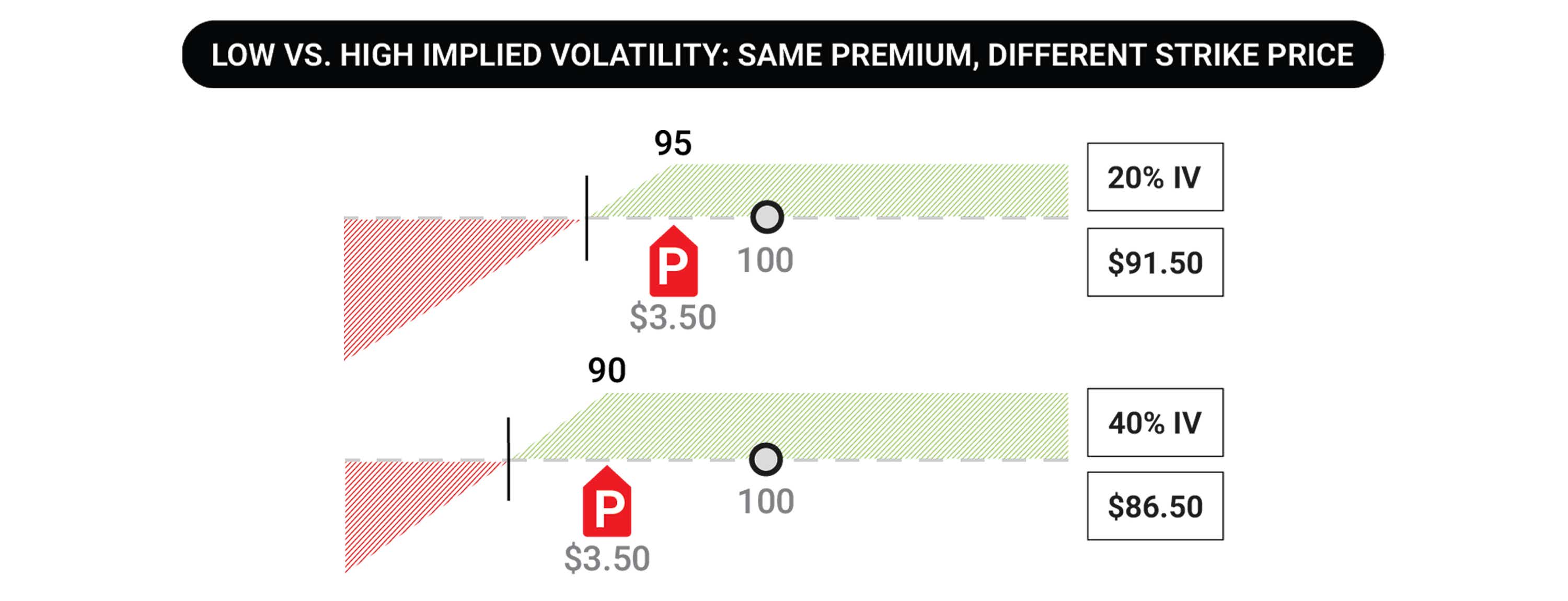
One cool thing about the standard deviation (SD) of a stock and implied volatility is that when IV is high, we can obtain these 1SD probabilities using much wider strikes.

In the example above, let’s say you want to sell a put at the 95 strike with XYZ stock trading at $100. If implied volatility is high, the strike may be worth $7.00, where my maximum profit is $700 if the strike expires OTM. If it goes ITM, you can use that $7 in premium to reduce my breakeven to $88 if I took the shares.

In a low IV environment, the same strike might only be trading for $3.50, which is half the extrinsic value compared to the high IV environment. This means you get only half of the maximum profit, and half of the breakeven reduction against the strike.

That’s the power of high implied volatility, and how it affects the trade entry price, and proximity of the strike price from the stock price.

 Identifying Options With Low Implied Volatility For Long Premium Strategies

When the implied volatility is low and the premiums are low-priced, it’s typically a buyers’ market.

In a low IV environment, you can consider options buying strategies such as:

• Debit spreads
• Naked long puts/calls
• Diagonal & calendar spreads

Let’s take a look at another example that shows the difference between a high and low IV environment:

Suppose you’re just looking to collect $3.50 in extrinsic value premium for selling a put, and you want to take the stock if the put goes in the money (ITM). In a high IV environment, you may be able to go to the $90 strike to collect that $3.50, and your breakeven would be at $86.50 if you took the shares.

In a low IV environment, you could be at the $95 strike to collect that same $3.50 in premium. That means your breakeven for the shares would be $91.50, a full 5 points higher than the high IV environment’s strike.

In the below implied volatility example, you’ll see that by factoring in IV, you only take a 16% risk and have an 84% chance of success, which is great for probability traders. To capture a 1SD move in a strangle or iron condor, we combine the 84% OTM short call with the 84% OTM short put, and define our risk further OTM as we see fit – which then gives us around a 68% probability OTM.

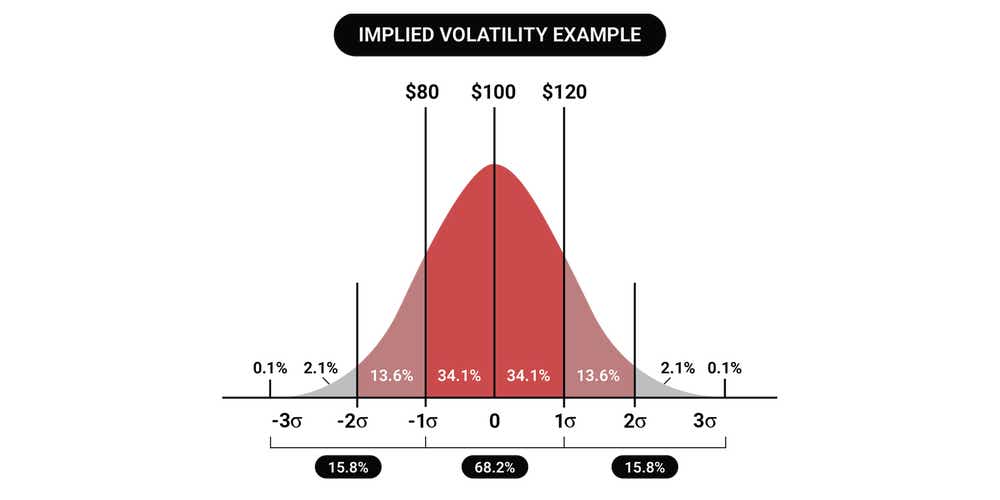
The dark red section in the implied volatility example shows that after 12 months (1SD), our stock that’s trading at $100, has a 68% chance of trading between $80 and $120. There is a chance that the stock will only be above $120, 16% of the time and below $80 also 16% of the time.

Here’s a practical scenario: 

Stock is trading at $50, and the implied volatility of the option contract is 20%. This implies there’s a consensus in the marketplace that a one SD move over the next 12 months will be plus or minus $10 (since 20% of the $50 stock price equals $10).

tastytrade, Inc. and tastylive, Inc. are separate but affiliated companies.